GAMES笔记

GAMES系列网络课程简要学习笔记

二次整理自网络教程。

计算机图形学与混合现实在线平台 – GAMES: Graphics And Mixed Environment Symposium

GAMES101 现代计算机图形学入门

闫令琪老师

GAMES101

参考书：Fundamentals of Computer Graphics 第四版

01 Overview of Computer Graphics

What is Computer Graphics?

• The use of computers to synthesize and manipulate visual information

Why study Computer Graphics?

• Applications
• Fundamental Intellectual Challenges
• Technical Challenges

Course Topics

• Rasterization
• Curves and Meshed
• Ray Tracing
• Animation / Simulation

GAMES101不教API和工具。

CV和CG是互逆的一对。

要求：Do not publish your code (on Github, etc.) for assignments using our skeleton code.

02 Review of Linear Algebra

Graphics' Dependencies

• Basic mathematics
  • Linear algebra, calculus, statisics
• Basic physics
  • Optics, Mechanics
• Misc
  • Signal processing
  • Numerical analysis
• And a bit of aesthetics

这节课主要复习基础线代，不再赘述。

03 Transformation

• Why study transformation
  • Modeling
  • Viewing

2D transformation

Scale Matrix: \[ \begin{pmatrix} x^{'} \\ y^{'} \end{pmatrix} = \begin{pmatrix} s_{x} & 0\\ 0 & s_{y} \end{pmatrix} \cdot \begin{pmatrix} x \\ y \end{pmatrix} \] Reflection Matrix: (with respect to the Y-axis) \[ \begin{pmatrix} x^{'} \\ y^{'} \end{pmatrix} = \begin{pmatrix} -1 & 0\\ 0 & 1 \end{pmatrix} \cdot \begin{pmatrix} x \\ y \end{pmatrix} \] Shear Matrix: (just like shear a square to a rhombus) \[ \begin{pmatrix} x^{'} \\ y^{'} \end{pmatrix} = \begin{pmatrix} 1 & a\\ 0 & 1 \end{pmatrix} \cdot \begin{pmatrix} x \\ y \end{pmatrix} \] Rotation Matrix: (about the origin(0,0), CCW by default) \[ \begin{pmatrix} x^{'} \\ y^{'} \end{pmatrix} = \begin{pmatrix} cos\theta & -sin\theta\\ sin\theta & cos\theta \end{pmatrix} \cdot \begin{pmatrix} x \\ y \end{pmatrix} \] 用顶点在原点的正方形在坐标轴上的另外两个顶点转一下就推导出来了。

Homogeneous coordinates

From (affine map = linear map + translation) \[ \begin{pmatrix} x^{'} \\ y^{'} \end{pmatrix} = \begin{pmatrix} a & b\\ c & d \end{pmatrix} \cdot \begin{pmatrix} x \\ y \end{pmatrix} + \begin{pmatrix} t_{x} \\ t_{y} \end{pmatrix} \] to (using homogenous coordinates) \[ \begin{pmatrix} x^{'} \\ y^{'} \\ 1 \end{pmatrix} = \begin{pmatrix} a & b & t_{x} \\ c & d & t_{y} \\ 0 & 0 & 1 \end{pmatrix} \cdot \begin{pmatrix} x \\ y \\ 1 \end{pmatrix} \]

2D Point = \((x, y, 1)^T\)

2D vector = \((x, y, 0)^T\)

• vector + vector = vector
• point - point = vector
• point + vector = point
• point + point = midpoint

\[ \begin{pmatrix} x \\ y \\ w \end{pmatrix} is\ the\ 2D\ Point \begin{pmatrix} x/w \\ y/w \\ 1 \end{pmatrix} ,\ w\ \ne\ 0 \]

How to rotate around a given point c?

1. Translate center to origin
2. Rotate
3. Translate back

矩阵乘法没有交换律但是有结合律。

04 Transformation Cont.

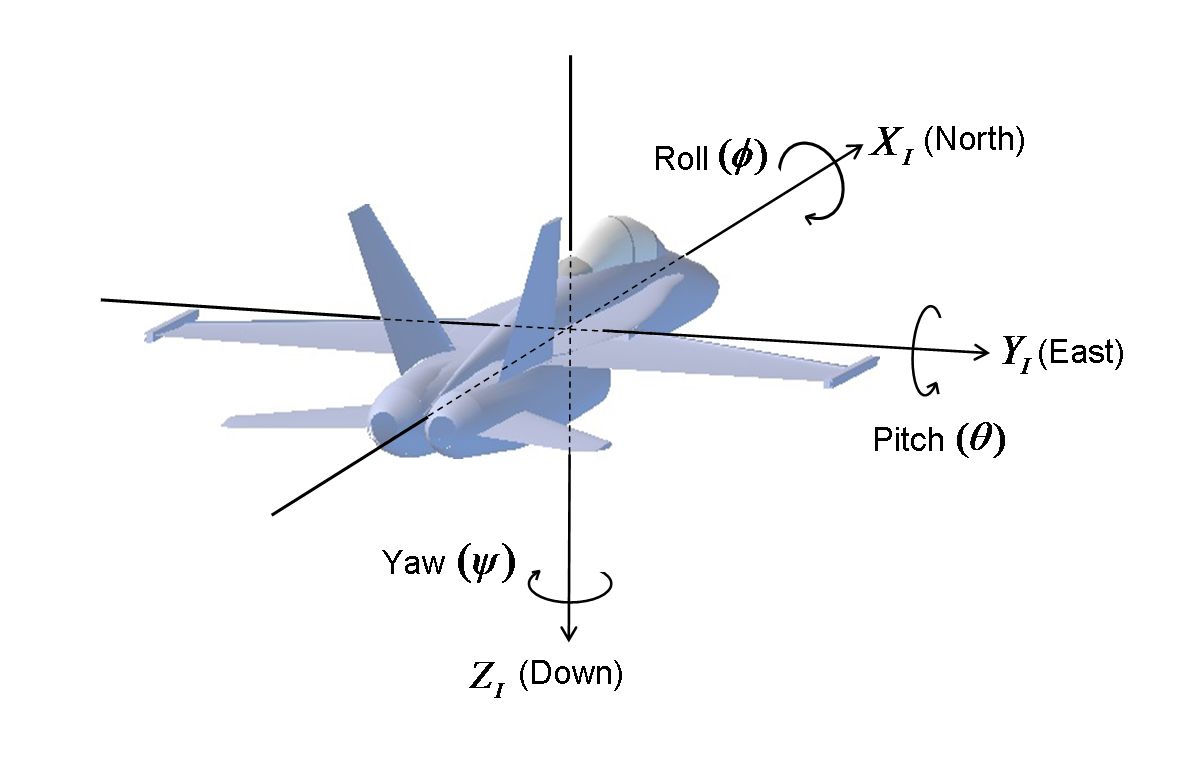
3D transformation

\[ R_{x}(\alpha)= \begin{pmatrix} 1 & 0 & 0 & 0\\ 0 & cos\alpha & -sin\alpha & 0\\ 0 & sin\alpha & cos\alpha & 0\\ 0 & 0 & 0 & 1 \end{pmatrix}\\ R_{y}(\alpha)= \begin{pmatrix} cos\alpha & 0 & sin\alpha & 0\\ 0 & 1 & 0 & 0\\ -sin\alpha & 0 & cos\alpha & 0\\ 0 & 0 & 0 & 1 \end{pmatrix}\\ R_{z}(\alpha)= \begin{pmatrix} cos\alpha & -sin\alpha & 0 & 0\\ sin\alpha & cos\alpha & 0 & 0\\ 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 1 \end{pmatrix} \]

按叉乘，\(y\times z=x\)，\(z\times x=y\)，\(x\times y=z\)，循环对称，所以y的旋转矩阵看上去和另外两个是相反的。

\[ R_{xyz}(\alpha,\beta,\gamma)=R_x(\alpha)R_y(\beta)R_z(\gamma) \] Rodrigues's Rotation Formula

Rotation by angle \(\alpha\) around axis \(n\) \[ R(n,\alpha)=cos(\alpha)I+(1-cos(\alpha))nn^T+sin(\alpha) \begin{pmatrix} 0 & -n_z & n_y \\ n_z & 0 & -n_x \\ -n_y & n_x & 0 \end{pmatrix} \]

Viewing transformation

View / Camera transformation

camera

• Position \(\vec{e}\) (origin)
• Look-at direction \(\hat{g}\) (Z axis)
• Up direction \(\hat{t}\) (Y axis)

\[ M_{view}=R_{view}T_{view}= \begin{bmatrix} x_{\hat{g}\times\hat{t} } & y_{\hat{g}\times\hat{t} } & z_{\hat{g}\times\hat{t} } & 0 \\ x_{t} & y_{t} & z_{t} & 0 \\ x_{-g} & y_{-g} & z_{-g} & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} 1 & 0 & 0 & -x_e \\ 0 & 1 & 0 & -y_e \\ 0 & 0 & 1 & -z_e \\ 0 & 0 & 0 & 1 \end{bmatrix} \]

Projection transformation

Orthographic projection

投影空间为cuboid，六个面延长之后分别与x轴交于l、r，与y轴交于t、b，与z轴交于n、f。 \[ M_{ortho}= \begin{bmatrix} \frac{2}{r-l} & 0 & 0 & 0 \\ 0 & \frac{2}{t-b} & 0 & 0 \\ 0 & 0 & \frac{2}{n-f} & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} 1 & 0 & 0 & -\frac{r+l}{2} \\ 0 & 1 & 0 & -\frac{t+b}{2}\\ 0 & 0 & 1 & -\frac{n+f}{2}\\ 0 & 0 & 0 & 1 \end{bmatrix} \] Perspective projection

投影空间为frustum，先挤压为cuboid，再Orthographic projection。 \[ M_{squish}= \begin{bmatrix} n & 0 & 0 & 0 \\ 0 & n & 0 & 0 \\ 0 & 0 & n+f & -nf \\ 0 & 0 & 1 & 0 \end{bmatrix} \] \[ M_{persp} = M_{ortho}M_{squish}= \begin{bmatrix} \frac{2n}{r-l} & 0 & \frac{l+r}{l-r} & 0 \\ 0 & \frac{2n}{t-b} & \frac{b+t}{b-t} & 0 \\ 0 & 0 & \frac{n+f}{n-f} & \frac{2nf}{f-n} \\ 0 & 0 & 1 & 0 \end{bmatrix} \\ \] 透视投影得到的点在齐次坐标系（称为在裁剪空间内），需要使用透视除法将该点从齐次坐标系转换到笛卡尔坐标系（称为在NDC（标准设备坐标）内）。透视除法将顶点四个分量都除以w。

05 Rasterization 1 (Triangles)

FOV（field of view）视场角计算方法：

水平FOV=2artan(胶片宽/2/镜头焦距）

垂直FOV=2artan(胶片高/2/镜头焦距）

MVP（Model、View、Projection）转换后在屏幕上光栅化成像。

屏幕空间即像素矩阵，每个像素看作一个小方块。

Viewport transform matrix: \[ M_{viewport}= \begin{pmatrix} \frac{width}{2} & 0 & 0 & \frac{width}{2}\\ 0 & \frac{height}{2} & 0 & \frac{height}{2}\\ 0 & 0 & 1 & 0\\ 0 & 0 & 0 & 1 \end{pmatrix} \] 与z不相关，在xy平面做变换：\([-1,1]^2\)到\([0,width]\times[0,height]\)。

光栅化设备部分参见虎书3.1笔记。

实际设备上每个像素由RGB三种感光元件组成。

光栅化方法：遍历像素，判断像素中心点是否在三角形内（叉积判断法）。可以用AABB（axis aligned bounding box）加速。

❓三角形公共边上的点属于哪个三角形：OpenGL和DirectX规定，如果有点落在三角形的上边和左边的话，认为这个点在三角形内，落在右边和下边，认为在三角形外。没有看懂。

06 Rasterization 2 (Antialiasing and Z-Buffering)

Sampling Artifacts的类型：

• Jaggies - sampling in space
• Moire - undersampling images
• Wagon wheel effect - sampling in time

讲了傅里叶变换和滤波（数字图像处理的知识）。

Antialiasing方法：

• 先Blurring再Sample，MSAA（Multisampling）。像素划分为更小的子像素后，像素颜色＝三角形颜色X三角形覆盖子像素数／总子像素数。
• FXAA（Fast Approximate）。图像后处理，找到边界并处理。
• TAA (Temporal) 。复用上一帧的结果，相当于将MSAA对应的样本分布在时间上。

超分和AA本质相似，因为超分也是在提高采样率。DLSS（Deep Learning Super Sampling）让AI来猜缺失的细节。

07 Shading 1 (illumination, Shading and Graphics Pipeline)

先讲上一节的Z-Buffer。

对每个像素存深度值z（正数），z越小越近（深度图中表现为越黑），z越大越远（深度图中表现为越白）。

每一帧对应一张深度图，深度值初始为无限大，遍历三角形更新深度图。复杂度为O(n)，n为三角形数量。由GPU硬件实现。

Shading

字典定义：The darkening or coloring of an ilustration or diagram with parallel lines or a block of color.

本课程定义：The process of applying a material to an object.

Shading部分讲了Blinn-Phong Reflectance Model，参见虎书笔记5.2、5.3。

08 Shading 2 (Shading, Pipeline and Texture Mapping)

Flat shading 每个面计算一次着色，一个三角形上所有点颜色相同。

Gouraud shading 每个顶点计算一次着色，三角形内部点颜色由顶点颜色插值得到。

Phong shading 每个像素计算一次着色，三角形内部点法线由顶点法线插值得到。

顶点法线由相邻面的法线求加权平均得到（权重为三角形面积）。

三角形插值时使用重心坐标。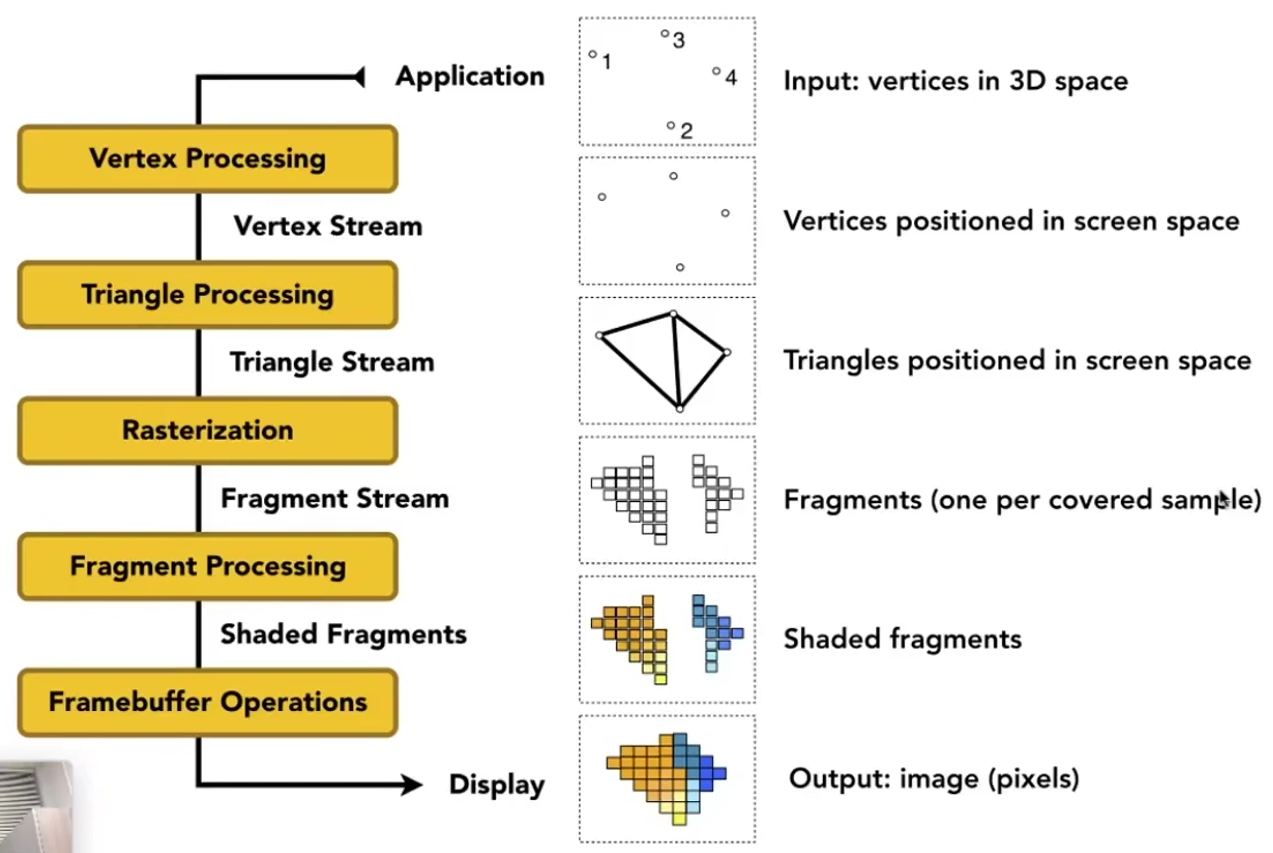

图形管线详细参见DX12龙书笔记第五章笔记。

shadertoy：在线着色器编写与渲染网站。

纹理映射即将二维表面蒙在三维物体表面。

Wang tile：一种生成可密铺纹理的算法。

09 Shading 3 (Texture Mapping Cont.)

A、B、C为三角形顶点坐标，对三角形所在平面上任意一点\((x,y)\)，重心坐标\(\alpha、\beta、\gamma\)代表： \[ (x,y)=\alpha A+\beta B+\gamma C \\ \alpha+\beta+\gamma=1 \] 重心坐标可由面积求得。例如，对于点P，\(\alpha=\frac{S_{PBC}}{S_{ABC}}\)。

透视投影是非线性的，因此透视投影或需要对重心坐标进行矫正。应从屏幕空间逆变换回三维空间，再用重心坐标插值。

纹理<平面，纹理放大：

• Nearest
• Bilinear
• Bicubic

纹理>平面，缩小导致摩尔纹，可以通过超采样解决（增大平面上每个点在纹理上的采样数，与MSAA类似）。工程中用mipmap预存范围查询的平均结果进行加速。

普通的mipmap范围查询区域为正方形，而实际区域并不规则，导致过模糊。用Anisotropic Filtering可以解决：

• Ripmaps and summed area tables
• EWA filtering

10 Geometry 1 (Induction)

先讲上一节的纹理应用。

环境贴图：

• Spherical Environment Map
• Cube Map

Bump/Normal mapping改变法线，不改变几何。

Displacement mapping改变几何。相比Bump/Normal边缘也可以看出变化，并且会产生自阴影。Displacement需要三角形网格足够细，DirectX的dynamic tessellation可以动态决定。

纹理可以定义3D Procedural Noise用于地形建模。

预计算AO纹理。

3D纹理和体渲染。

几何表示方法

Implicit：

• algebraic surface
• level sets
• distance functions
• Constructive Solid Geometry
• Fractals（分形）

Explicit：

• point cloud
• polygon mesh
• subdivision, NURBS

11 Geometry 2 (Curves and Surfaces)

介绍了The Wavefront Object File (.obj) 的格式。

Curves

• Bezier curves
  • De Casteljau’s algorithm 绘制
  • quadratic Bezier 三控制点
  • Cubic Bézier Curve 四控制点
• B-splines
  • 贝塞尔曲线的扩展，具有局部性

Surfaces

• Bezier surfaces
• Triangles & quads (subdivision, simplification, regularization)
  • regularization指让三角形网格都接近正三角形。

12 Geometry 3

Subdivision

1. 拆分三角形
2. 调整顶点位置

Loop Subdivision（Loop是作者姓氏，无循环义）（仅适用三角形网格）

Catmull-Clark Subdivision（适用有四边形也有三角形的网格）

Simplification

edge collapsing，最小化Quadric Error Metrics（新的点到原本几个面的距离平方和达到最小）。

Shadow Mapping

An Image-space Algorithm，不知道场景几何信息，需要处理走样。只能做硬阴影，有数值精度问题。

1. 在光源处用虚拟摄像机光栅化，对每一点得到深度a
2. 在摄像机处光栅化，成像的点投影回光源处，得到深度b
3. 摄像机光栅化得到的图像上a和b不同的点则有阴影

软阴影有过渡。物理上所称的半影（Penumbra）：

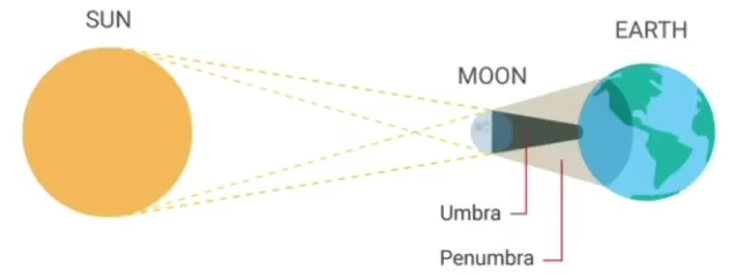
软阴影的产生是因为光源有一定的大小，点光源无法产生软阴影。

13 Ray Tracing 1 (Whitted-Style Ray Tracing)

光栅化的缺点：不能很好的处理全局效果（Soft shadows、Glossy reflection、Indirect illumination）。

光线追踪准确而且质量高，但是慢。

Basic Ray-Tracing Algorithm

从相机出发向世界中投射光线（Ray Casting），判断是否对光源可见。（光路可逆）

Whitted-Style Ray Tracing

投射光线后多次弹射（反射或折射），像素值为多个弹射点的着色值之和。

• primary ray：投射的第一根光线
• secondary rays：一次弹射之后的光线
• shadow rays：和光源相连判断可见性的光线

关键问题：Ray-Surface Intersection

14 Ray Tracing 2 (Acceleration & Radiometry)

AABB：划分为均匀格子，需要考虑划分密度。（Heuristics：常数27乘以3D场景中物体的数量）

Oct-Tree：每次均八分，直到格子里为空或物体足够少。

KD-Tree：每次二分（不均分，但轴对齐）。

BSP-Tree： 每次二分（不均分，且不轴对齐）。

BVH（Bounding Volume Hierarchy ）：按物体划分。

BVH优点：

1. 一个几何只出现在一个叶子节点里
2. 不用求几何和包围盒的交

辐射度量学（Radiometry）

辐射能（radiant energy）\(Q\)：\(J\)。

辐射通量（radiant flux）\(\Phi\)：\(W\)（即\(J/s\)）或\(lm\)。

辐射强度（radiant Intensity）\(I\)：\(W/sr\)或\(cd\)。\(cd\)是七个SI单位之一。

辐照度（irradiance）\(E\)：\(W/m^2\)或\(lux\)

辐射率（radiance）\(L\)：\(W/(m^2\cdot sr)\)或\(nit\)

BRDF值\(f\)：\(sr^{-1}\) （\(L/E\)）

15 Ray Tracing 3 (Light Transport & Global llumination)

渲染方程（反射方程+自发光项）： \[ L_r(x,w_r)=L_e(x,w_r)+\int_{\Omega}L_i(x,w_i)f(x,w_i,w_r)\cos \theta_id\omega_i \]

reflected light = emission + integral of Incident light * BRDF * cosine of incident angle

简化： \[ L=E+KL \\ L=(1-K)^{-1}E \\ \] 泰勒展开： \[ L=(1+K+K^2+K^3+...)E \] 幂指数即弹射次数。

回顾了一下概率论。

16 Ray Tracing 4 (Monte Carlo Path Tracing)

介绍了蒙特卡洛积分。

Whitted-Style Ray Tracing缺陷：

• 对于镜面反射正确，对于glossy反射错误（没有考虑粗糙度）。
• 在漫反射表面就停止了，不继续弹射，没有Color bleeding。

用蒙特卡洛积分解渲染方程： \[ \int_{\Omega}L_i(x,w_i)f(x,w_i,w_r)\cos\theta_id\omega_i\approx \frac{1}{N}\sum_{i=1}^{N}\frac{L_i(x,w_i)f(x,w_i,w_r)\cos\theta_i}{p(w_i)} \] \(p(w_i)\)即PDF，若对半球均匀采样，\(p(w_i)=\frac{1}{2\pi}\)。

取N=1，并随机停止追踪，避免计算量爆炸。

SPP（samples per pixel）：一个像素打出多少光线。

若光源小，SPP过低会出现大量噪点，打不到光源。在光源上采样PDF可以避免浪费光线： \[ dw=\frac{dAcos\theta'}{\left \|x^{'}-x\right \|^2} \] \(A\)是光源面积，\(x^{'}\)是光源位置，\(x\)是着色点位置，\(\theta'\)是着色点与光源连线与光源法线的夹角。

Modern Concepts：

• (unidirectional & bidirectional) path tracing
• Photon mapping
• Metropolis light transport
• VCM/UPS (vertex connection merging/unified path sampling)
• UPBP (unifying points, beams, and paths in volumetric light transport simulation)

17 Materials and Appearances

Material==BRDF

Diffuse / Lambertian Material（BRDF）

\(\rho\)为albedo，对于理想漫发射，BRDF值\(f_r=\frac{\rho}{\pi}\)，是因为能量守恒的要求： \[ \begin{align} &\int_{\Omega} f_r \cos\theta_i \, \mathrm{d}\omega_i \\ =& f_r \int_{\Omega} \cos\theta_i \, \mathrm{d}\omega_i \\ =& f_r \int_{0}^{2\pi} \int_{0}^{\frac{\pi}{2}} \cos\theta \sin\theta\mathrm{d}\theta\mathrm{d}\phi \\ =& f_r \cdot \int_{0}^{2\pi} \mathrm{d}\phi \cdot \int_{0}^{\frac{\pi}{2}} \cos\theta \sin\theta\mathrm{d}\theta \\ =& f_r \times 2\pi \times \frac{1}{2} \\ =& f_r \times \pi \\ \end{align} \\ \] Glossy material（BRDF）

Blinn–Phong model：

\[ f_r=k_smax(0,n\cdot h)^p \] Ideal reflective / refractive material (BSDF)

Caustics（焦散：不准确的翻译，因为成因是聚焦，和散射没关系）：海水表面凹凸不平，光线向不同方向折射，在海底聚焦。

Snell’s Law \[ \eta_isin\theta_i=\eta_tsin\theta_t \] index of refraction (IOR) for incident ray \(\eta_i\)

index of refraction (IOR) for exiting ray \(\eta_t\)

\(\eta_i>\eta_t\)时没有折射。

Snell’s Window：从水下看上去，180度的视角被压成97.2度的光锥。由光线进入水中的大角度折射引起的。

Fresnel Reflection / Term：表示反射折射之比，Schlick’s approximation： \[ R_0=(\frac{n1-n2}{n1+n2})^2 \] \[ R(\theta)=R_0+(1-R_0)(1-cos\theta)^5 \] Torrance-Sparrow microfacet model

\[ f_r=\frac{F(l,h)G(l,v,h)D(h)}{4(n\cdot l)(n\cdot v)} \] F是Fresnel Term。

G是Shadowing Masking，如果没有G，球的边界（grazing angle）会非常亮。

D是Distribution of Normals，计算有多少微面元的法线m满足m=h（入射出射半向量）。

Properties of BRDFs

• Non-negativity
• Linearity（拆分之后计算再相加，例如diffuse、specular、ambient）
• Reciprocity principle
• Energy conservation
• Isotropic / Anisotropic（Isotropic BRDF少一个自由度，为3维）

Measuring BRDFs

MERL BRDF Database

18 Advanced Topics in Rendering

Advanced Light Transport

Unbiased light transport methods

Bidirectional path tracing (BDPT)

从光源和相机都出发，生成半路径（light sub-paths），连接成完整路径。

当光线传播在光源这半边比较容易算的时候（直接照亮场景中一小块区域，其它区域都是间接光照亮），BDPT的效果会更好，但速度相对慢。不能处理SDS。

Caustics的路径SDS（specular-diffuse-specular）。

Metropolis light transport (MLT)

因为采样的PDF和要积分的函数形状一致时方差最小。使用Markov Chain的蒙特卡洛方法。

适合Caustics。积分复杂，难以理论上分析渲染速度。具有局部性，有些像素收敛快，有些像素收敛慢，图像看上去脏，并且每一帧间有抖动，不适合做动画。

Biased light transport methods

Photon mapping

1. 从光源出发发射光子，在diffuse表面停止。
2. 从相机出发发射路径，在diffuse表面停止。
3. 局部密度估计。对一个着色点，取周围最近的N个光子，用光子的数量N除以它们占的面积A。有偏是因为\(dN/dA!=\Delta N/\Delta A\)。虽然有偏（biased）但一致（consistent），指样本数量接近无限时期望收敛到正确结果。

Vertex connection and merging (VCM)

BDPT和Photon mapping的结合。前者不能处理SDS，后者处理diffuse不如前者，互补。

Instant radiosity

(IR) (many light methods)

Unbiased.

已经被照亮的地方都可以认为它们是光源，Virtual Point Light (VPL)。看到着色点后用所有VPL照亮。

窄的缝隙产生错误的发光，因为光源与着色点过近。不能做glossy。

Advanced Appearance Modeling

Non-surface models

Participating media

散射介质，如云、雾。

Hair / fur / fiber

头发表面有两种高光，一种无色发白，一种有色。按照Marschner Model，Reflection记作R、Transmission记作T，有R、TT、TRT三种光线。（BCSDF）

毛发有cuticle（表皮）、cortex（皮层）、Medulla（髓质）三层结构，，动物毛发结构和人的头发髓质大小不同。

Granular material

颗粒状，如盐、糖等。

Surface models

Translucent material (BSSRDF)

translucent不应翻译为半透明（semitransparent）。

semitransparent：沿着一个方向传播并被吸收。

translucent：光线从一个面进入，从另一个面离开，可以被导到其它方向去。

Cloth

fiber缠绕成ply（股），ply缠绕成yarn（线），线编织成布。

1. 当成participating media渲染
2. 渲染每一根fiber

Detailed material (non-statistical BRDF)

若使用分辨率极高的法线贴图，渲染十分困难。

考虑一个像素会覆盖很多的微表面，将微表面的分布拿出来（在一个小范围内的微表面的法线分布NDF算出来），替代原本光滑的分布，用在微表面模型里。

引入波动光学：衍射和干涉现象。

Procedural appearance

不使用纹理，使用噪声函数，随用随取。

19 Cameras, Lenses and Light Fields

Imaging = Synthesis + Capture

Camera

Sensor记录的是irradiance。

针孔相机拍不出景深。透镜相机才可以。光追用的针孔相机。

05节笔记记载了FOV的计算方法。人们通常以35mm格式的胶片（film）为基准，固定传感器的大小，再通过定义焦距的方式来定义FOV。比如，17mm焦距对应广角104度。手机的胶片小很多，显示的是等效焦距（若胶片为基准胶片）。

影响Exposure（曝光）：

• Aperture size 光圈的大小
• Shutter speed 快门速度
• ISO gain ISO 增益/感光度

Lens

现代成像使用透镜组。

Ideal Thin Lens：

1. All parallel rays entering a lens pass through its focal point.
2. All rays through a focal point will be in parallel after passing the lens.
3. Focal length can be arbitrarily changed.

The Thin Lens Equation： \[ \frac{1}{f}=\frac{1}{z_i}+\frac{1}{z_o} \] 物距\(z_o\)，像距\(z_i\)，焦距\(f\)。

Defocus Blur

可解释景深。

一个点穿过透镜后，若像距对应成像平面远离真实的成像平面，会形成Circle of Confusion (CoC)。

F数（F-Stop）\(N=f/D\)，焦距/光圈直径。CoC大小和F数成反比。

光圈通过挡透镜动态改透镜的大小。

Depth of Field

景深。CoC很小的一段范围内对应的场景的一段是清晰的。

20 Color and Perception

Light Field / Lumigraph

SIGGRAPH 2012 course on light fields

The Plenoptic Function \[ P(\theta,\phi,\lambda,t,V_x,V_y,V_z) \] 光场是全光函数的一小部分，描述任何一个位置的一个方向的光强。

光场是四维函数，使用二维位置（\(uv\)）和二维方向（\(\theta\phi\)）。

光照相机每个像素对应一个微透镜，拍摄的照片实际上记录了光场，可以重新聚焦得到普通相机照的照片。

Color

光谱：谱功率密度（SPD，Spectral Power Distribution），不同的波长的强度，\(W/nm\)。SPD满足加法定律。

颜色是human perception。

讲了人眼的结构。视网膜上的Rods（视杆细胞）感知光强，Cones（视锥细胞）感知颜色。Cones分为S、M、L三种，分别感知短波长、中间波长、长波长。

同色异谱（Metamerism）：光谱不同看到的颜色相同。显示器利用此原理。

Color Reproduction / Matching

红黄蓝三原色减色混合得到其它的颜色。显示器使用红绿蓝的加色混合。

讲了sRGB、CIE XYZ、HSV、CIE LAB颜色空间。

印刷中使用CMYK（Cyan青、Magenta品红、Yellow黄、Key黑）减色系统。使用黑色是因为成本低。

21 Animation

讲了动画的历史。

Keyframe Animation

Physical Simulation

• Newton’s Law
• Mass Spring System
• Particle Systems
• Simulated Flocking as an ODE

Kinematics

• Forward Kinematics
• Inverse Kinematics

Rigging

对物体或角色的不同地方加一些控制点

22 Animation Cont.

Single particle simulation

• Explicit Euler method
• Instability and improvements

Rigid body simulation

Fluid simulation

• A Simple Position-Based Method
• Eulerian vs. Lagrangian
• Material Point Method

GAMES104 现代游戏引擎入门必修课

王希老师

GAMES104

BoomingTech/Piccolo: Piccolo (formerly Pilot) – mini game engine for games104

GAMES202 高质量实时渲染

闫令琪老师

GAMES202