估计

二次整理自课程学习。

Parameter Estimation

假定概率密度的特定形式（比如高斯分布），只需要估计参数（比如均值、方差）即可。比如Bayes和ML。

Criterion for Classification Decision Rule：

MAP (Maximum A Posteriori) Criterion
ML (Maximum Likelihood) Criterion
Bayes Criterion
Other Criterion

假定总体$X$的PDF为$f(x\mid\theta)$，观测到一组样本$(X_1,X_2,...,X_n)=(x_1,x_2,...,x_n)$，需要估计参数$\theta$。

Bayes

贝叶斯估计是贝叶斯学派观点。$\theta$是随机的，只能估计其分布。 \[ \pi (\boldsymbol \theta|\boldsymbol x)=\frac {f(\boldsymbol x|\boldsymbol \theta)\pi (\boldsymbol \theta)}{m(\boldsymbol x)}=\frac {f(\boldsymbol x|\boldsymbol \theta)\pi (\boldsymbol \theta)}{\int f(\boldsymbol x|\boldsymbol \theta)\pi (\boldsymbol \theta)d(\boldsymbol \theta)} \] $() $为参数$ $ 的先验分布（prior distribution），表示对参数$ $的主观认识，是非样本信息。$ (|x) $为参数$ $的后验分布（posterior distribution）。因此，贝叶斯估计可以看作是，在假定$ $服从 $\pi (\boldsymbol \theta)$ 的先验分布前提下，根据样本信息去校正先验分布，得到后验分布 $\pi (\boldsymbol \theta|\boldsymbol x)$ 。由于后验分布是一个条件分布，通常我们取后验分布的期望作为参数的估计值。

使用贝叶斯风险用来度量一个估计量的好坏。对于待估参数$\theta$和$x$，参数$\theta$的贝叶斯估计值为$\hat{\theta}$，那么贝叶斯风险为： \[ \R=E_{\theta,x}[l(\theta,\hat{\theta})] \] $l$为评价风险的损失函数。

MAP

可以看作Bayes的特殊情况。

贝叶斯估计中后验分布的计算往往是非常棘手的。最大后验（MAP）估计利用了无法从观测样本获得的来自先验的信息，是贝叶斯估计的一种近似解。使后验分布$\pi (\boldsymbol \theta|\boldsymbol x)$极大化的$\hat{\theta}_{map}$是$\theta$的MAP估计值。 \[ \boldsymbol {\hat \theta}_{map}=arg \underset {\boldsymbol \theta}{\max} \pi (\boldsymbol \theta|\boldsymbol x)=arg \underset {\boldsymbol \theta}{\max} \frac {f(\boldsymbol x|\boldsymbol \theta)\pi (\boldsymbol \theta)}{m(\boldsymbol x)}=arg \underset {\boldsymbol \theta}{\max} {f(\boldsymbol x|\boldsymbol \theta)\pi (\boldsymbol \theta)}=arg \underset {\boldsymbol \theta}{\max} (\log {f(\boldsymbol x|\boldsymbol \theta)+ \log \pi (\boldsymbol \theta))} \] 如果将机器学习结构风险中的正则化项对应为上式的$\log \pi (\boldsymbol \theta)$，那么带有这种正则化项的ML学习就可以被解释为MAP。

ML

可以看作MAP的特殊情况。

极大似然（ML）估计是频率学派观点。$\theta$客观存在，只是未知。

使样本$(X_1,X_2,...,X_n)=(x_1,x_2,...,x_n)$更容易观测到（发生概率更大）的$\hat{\theta}_{ml}$是$\theta$的ML估计值。 \[ L(\boldsymbol \theta|\boldsymbol x)=f(\boldsymbol x|\boldsymbol \theta)=f(x_1,x_2,\dots,x_n|\boldsymbol \theta)=\prod^{n}_{i=1}f(x_i|\boldsymbol \theta) \] \[ \boldsymbol {\hat \theta}_{mle}=arg\underset {\boldsymbol \theta}{\max} L(\boldsymbol \theta|\boldsymbol x) \]

eg. MAP&ML

拿到一枚未知的硬币，估计其正面出现概率$\theta$。

观测到样本$X$：反正正正正反正正正反

似然函数：$f(X\mid\theta)=(1-\theta)\times\theta\times\theta\times\theta\times\theta\times(1-\theta)\times\theta\times\theta\times\theta\times(1-\theta)=\theta^7(1-\theta)^3$

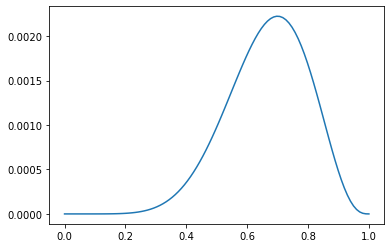
求$f(X\mid\theta)$图像和使其最大的$\theta$值：

import numpy as np
import matplotlib.pyplot as plt

x = np.linspace(0,1,100)
y = x**7*(1-x)**3

plt.plot(x,y)
plt.show()

print(x[y.argmax()])

0.696969696969697

得出使其最大的$\theta$大约是0.7。此即ML估计。

引入$\theta$的先验分布为高斯分布，即$f(\theta)$为均值0.5，方差0.1的高斯函数。 \[ f(\theta)=\frac{1}{\sigma\sqrt{2\pi}}e^{-\frac{(\theta-\mu)^2}{2\sigma^2}},\mu=0.5,\sigma=0.1 \] 求$f(X\mid\theta)f(\theta)$图像和使其最大的$\theta$值：

import numpy as np
import matplotlib.pyplot as plt

x = np.linspace(0,1,100)
y = x**7*(1-x)**3

sigma = 0.1
mu = 0.5
gauss = 1/(sigma * np.sqrt(2*np.pi)) * np.power(np.e,-((x-mu)**2)/(2*sigma**2))
y *= gauss

plt.plot(x,y)
plt.show()

print(x[y.argmax()])

0.5555555555555556

得出使其最大的$\theta$大约是0.56。此即MAP估计。

Mixture models

以Gaussian mixture model为例，一个复杂的曲线可以用若干个组合起来的高斯函数来逼近。

EM

当模型的变量都是观测变量时，可以直接通过前面的ML、MAP估计模型参数。但是当模型包含隐变量时，就不能简单的使用这些估计方法。比如K-means算法，除了给定的样本（也就是观测变量）$X$以及参数$\theta$ （也就是那些聚类的中心）之外，还包含一个隐变量（记为$Z$，每个样本的所属类别）。

Expectation-Maximum是最常见的隐变量估计方法，在机器学习中有极为广泛的用途，例如常被用来学习GMM的参数、隐式马尔科夫算法（HMM）、LDA主题模型的变分推断等等。

给定一组观测数据记为$X=(x_1,x_2,\dots,x_n)$ 及参数 $\theta$ 。因为 $x_1,x_2,\dots,x_n$ 是独立同分布，所以有以下对数似然函数： \[ \begin{align} \ell(\theta|X)&=\log{P\left(X|\theta\right)} =\log\left( \prod_{i=1}^n P\left(x_i|\theta\right) \right) =\sum_{i=1}^n \log P(x_i|\theta) \end{align} \] 可以通过极大似然估计来求解最优参数，即： \[ \begin{align} \hat{\theta}&=\arg \max_\theta \log{\ell\left(\theta|X\right)} =\arg \max_\theta \sum_{i=1}^n \log P(x_i|\theta) \end{align} \] 但是由于隐变量的存在， $\log{P\left(X|\theta\right)}$ 变为 \[ \begin{align} \log{P\left(X\middle|\theta\right)}&=\log{\sum_{Z}\ P\left(X,Z|\theta\right)}\\ &=\log{\left(\sum_{Z}\ P\left(X|\theta,Z\right)P\left(Z|\theta\right)\right)} \end{align} \] 下面构造一个容易优化的——关于对数似然函数的——下界函数，通过不断的优化这个下界，迭代逼近最优参数。

引入隐变量 $Z$ 的概率分布 $q(Z)$ ，满足 \[ \sum_Z q(Z)=1 \] 并且以下等式成立 \[ P\left(X|\theta\right)=\frac{P\left(X,Z|\theta\right)}{P\left(Z|X,\theta\right)}=\frac{P\left(X,Z|\theta\right)/q\left(Z\right)}{P\left(Z|X,\theta\right)/q\left(Z\right)} \] 两边同时取对数 \[ \begin{align} \log{P\left(X|\theta\right)}&=\log{\frac{P\left(X,Z|\theta\right)/q\left(Z\right)}{P\left(Z|X,\theta\right)/q\left(Z\right)}} \end{align} \] 同时求两边在 Z 上的期望 \[ \mathbb{E}_Z\left[\log{P\left(X|\theta\right)}\right]=\mathbb{E}_Z\left[\log{\frac{P\left(X,Z|\theta\right)/q\left(Z\right)}{P\left(Z|X,\theta\right)/q\left(Z\right)}}\right] \] 因为 $\log{P\left(X|\theta\right)}$ 与 Z 无关，所以求期望仍然不变： \[ \begin{align} \mathbb{E}_Z\left[\log{P\left(X|\theta\right)}\right]&=\sum_{Z}{q\left(Z\right)\log{P\left(X|\theta\right)}}\\ &=\log{P\left(X|\theta\right)}\sum_{Z} q\left(Z\right)\\ &=\log{P\left(X|\theta\right)} \end{align} \] 然后将右边展开 \[ \begin{align} \mathbb{E}_Z\left[\log{\frac{P\left(X,Z|\theta\right)/q\left(Z\right)}{P\left(Z|X,\theta\right)/q\left(Z\right)}}\right]&=\sum_{Z}{q\left(Z\right)\log{\frac{P\left(X,Z|\theta\right)/q\left(Z\right)}{P\left(Z|X,\theta\right)/q\left(Z\right)}}}\\ &=\sum_{Z}{q\left(Z\right)\log{\frac{P\left(X,Z|\theta\right)}{q\left(Z\right)}}}-\sum_{Z}{q\left(Z\right)\log{\frac{P\left(Z|X,\theta\right)}{q\left(Z\right)}}}\\ &=\sum_{Z}{q\left(Z\right)\log{\frac{P\left(X,Z|\theta\right)}{q\left(Z\right)}}}+\sum_{Z}{q\left(Z\right)\log{\frac{q\left(Z\right)}{P\left(Z|X,\theta\right)}}}\\ &=\sum_{Z}{q\left(Z\right)\log{\frac{P\left(X,Z|\theta\right)}{q\left(Z\right)}}}+KL\left(q\left(Z\right)||P\left(Z|X,\theta\right)\right)\\ &\geq\sum_{Z}{q\left(Z\right)\log{\frac{P\left(X,Z|\theta\right)}{q\left(Z\right)}}} \end{align} \]

相对熵 $KL\left(p||q\right)=\sum_{x\in X}{p\left(x\right)log{\frac{p\left(x\right)}{q\left(x\right)}}}$

由此得到对数似然函数的下界。并且当 $KL\left(q\left(Z\right)||P\left(Z|X,\theta\right)\right) = 0$，上式可以取到等号，由相对熵的性质可知，相对熵为0，也就是 $q(Z)=P(Z|X,\theta)$。

其中 $q(Z)$ 是$Z$的概率分布，但是因为无法观测$Z$ ，所以$q(Z)$未知，可以假设其等于 $P(Z|X,\theta)$ ，也就是$Z$关于给定$X$与$\theta$的后验，且$\theta$是由初始值$\theta^{(0)}$ 一次次迭代计算而来，所以此处的 $\theta$ 是迭代$i$次后的值。 \[ q(Z) = P(Z|X,\theta^{(i)}) \] 以上，就是EM算法中E步的由来。

然后通过极大似然估计得到： \[ \begin{align} \hat{\theta}&=\arg{\max_\theta{\sum_{Z}{q\left(Z\right)\log{\frac{P\left(X,Z|\theta\right)}{q\left(Z\right)}}}}}\\ &=\arg{\max_\theta{\sum_{Z}{P\left(Z|X,\theta^{\left(i\right)}\right)\log{\frac{P\left(X,Z|\theta\right)}{P\left(Z|X,\theta^{\left(i\right)}\right)}}}}}\\ &=\arg{\max_\theta{\sum_{Z}\ P\left(Z|X,\theta^{\left(i\right)}\right)\left(\log{P\left(X,Z|\theta\right)}-\log{P\left(Z|X,\theta^{\left(i\right)}\right)}\right)}}\\ &=\arg{\max_\theta{\sum_{Z}{P\left(Z|X,\theta^{\left(i\right)}\right)\log{P\left(X,Z|\theta\right)}}}}\\ &=\arg{\max_\theta{\mathbb{E}_{Z|X,\theta^{\left(i\right)}}\left[\log{P\left(X,Z|\theta\right)}\right]}} \end{align} \] 令$\hat{\theta}= \theta^{(i+1)}$，就得到了M步的公式 \[ \theta^{(i+1)}=\arg{\max_\theta{\mathbb{E}_{Z|X,\theta^{\left(i\right)}}\left[\log{P\left(X,Z|\theta\right)}\right]}} \] EM算法可以保证收敛到一个稳定点，但是却不能保证收敛到全局的极大值点，因此它是局部最优的算法。

eg. EM

假设我们有A，B两枚硬币，其中正面朝上的概率分别为$\theta_{A},\theta_{B}$，这两个参数即为需要估计的参数。我们设计5组实验，每次实验投掷5次硬币，但是每次实验都不知道用哪一枚硬币进行的本次实验。投掷结束后，会得到一个数组 $x=(x_{1},x_{2},...,x_{5})$ ，表示每组实验有几次硬币正面朝上，因此 $0\leq x_{i}\leq 5$ 。

虽然我们不知道每组实验用的是哪一枚硬币，但如果我们用某种方法猜测每组实验是哪个硬币投掷的，我们就可以将数据缺失的估计问题转化成一个最大似然问题和完整参数估计问题。

实验结果：

实验编号	结果
1	3正2反
2	2正3反
3	1正4反
4	3正2反
5	2正3反

首先，随机选取 $\theta_{A},\theta_{B}$的初始值，比如 $\theta_{A}=0.2,\theta_{B}=0.7$ 。

E步

计算在当前的预估参数下，隐变量（是A硬币还是B硬币）的每个值出现的概率。

对于第一组实验，3正面2反面。

如果是A硬币得到这个结果的概率为： $0.2^3\times0.8^2=0.00512$
如果是B硬币得到这个结果的概率为： $0.7^3\times0.3^2=0.03087$

因此，第一组实验结果是A硬币得到的概率为：$0.00512 / (0.00512 + 0.03087)=0.14$，第一组实验结果是B硬币得到的概率为：$0.03087/ (0.00512 + 0.03087)=0.86$。

整个5组实验的A,B投掷概率如下：

实验编号	是A硬币的概率	是B硬币的概率
1	0.14	0.86
2	0.61	0.39
3	0.94	0.06
4	0.14	0.86
5	0.61	0.39

M步

计算硬币投掷正反的期望：

实验编号	A硬币下正/反期望	B硬币下正/反期望
1	0.42 0.28	2.58 1.72
2	1.22 1.83	0.78 1.17
3	0.94 3.76	0.06 0.24
4	0.42 0.28	2.58 1.72
5	1.22 1.83	0.78 1.17
总计	4.22 7.98	6.78 6.02

通过计算期望把隐变量（是A硬币还是B硬币）消除掉了。 \[ \theta_{A} =4.22/(4.22+7.98)=0.35 \] \[ \theta_{B} =6.78/(6.78+6.02)=0.5296875 \] 这一步中，我们根据E步中求出的A硬币、B硬币概率分布，依据最大似然概率法则去估计$\theta_{A},\theta_{B}$。

最后，一直循环迭代E步M步，直到$\theta_{A},\theta_{B}$不更新为止。