Eliminating Cycles in Weak Tables【译】

释放弱表中的循环引用

Eliminating Cycles in Weak Tables

Barros A, Ierusalimschy R. Eliminating Cycles in Weak Tables[J]. J. Univers. Comput. Sci., 2008, 14(21): 3481-3497.

个人翻译并注释。

作者：

• Alexandra Barros，里约热内卢天主教大学， alexandra.barros@gmail.com
• Roberto Ierusalimschy，里约热内卢天主教大学，roberto@inf.puc-rio.br

Roberto Ierusalimschy是Lua的创造者之一（Roberto Ierusalimschy、Waldemar Celes、Luiz Henrique de Figueiredo在1993年于巴西里约热内卢天主教大学创造Lua），也是Programming in Lua的作者（中文版即Lua程序设计（第4版））。

摘要：弱引用构成了应用程序与其GC（Garbage collector）交互的一种优雅机制。在大多数典型用途中，弱引用是通过弱表（如Java的WeakHashMap）使用的。但是，大多数弱表的实现都有一个严重的限制：弱表中键和值之间的循环引用会阻止循环内的元素被回收，即使它们不再可以从外部访问到。这给在某些类型的应用程序中使用弱表带来了困难。

本文中，我们介绍了在Lua中解决此问题的方法。我们的方法包括将ephemerons机制适配到表中。我们修改了Lua虚拟机的GC以支持此机制。使用这个经过调整的GC，我们可以验证这个实现在解决Lua中弱表上的循环问题方面的效率和有效性。

ephemeron于Lua5.2引入，Lua程序设计（第4版）P263中将其译为“ 瞬表”。按照本文，ephemeron指改进后的弱对，个人感觉将ephemeron翻译为瞬项、将ephemerons table翻译为瞬表更加合理。为避免歧义，不对ephemeron做翻译。如property和attribute等其它术语也不翻译。

关键词：GC，弱表，弱引用

分类：D.3.3

1 Introduction

具有自动内存管理功能的编程语言通常会在客户端程序和GC之间提供一个接口。该接口由允许客户端程序与GC交互的机制组成，常见代表是finalizer¹²³⁴和弱引用（weak reference）⁵。

finalizer是GC在回收对象占用的内存之前自动执行的一种特殊方法。此类方法用于许多活动，包括管理对象缓存、释放服务器和其他程序提供的资源。终结器具有异步特性。Bloch⁶认为finalizer不可预测，通常很危险且不必要，并会对程序性能产生负面影响。但Boehm⁷认为finalizer的使用在某些情况下是必要的，并且其异步性并不一定会使程序不健全。

弱引用是一种不保护对象不被GC回收的引用。许多具有GC功能的编程语言至少从80年代开始就为弱引用提供了一些支持⁸⁹。弱引用还可以用作finalization机制，从而避免与传统finalizer相关的诸多问题。根据编程语言和其GC管理的方式，对终结器的支持甚至可能不再必要。

弱引用的重要性日益增加，促使我们寻找一个关键问题的解决方案：弱表中的循环。此问题的一个典型示例为property表中。通常，我们希望动态地向对象添加property，并且独立于它的类attribute。一种非常常见的方法是使用property表。在property表中，将对于对象的引用作为搜索键插入，与此键关联的值指定额外property。但是，如果property表中的所有引用都是普通的，则插入新的键/值对这一简单事实将阻止键引用的对象被收集。解决此问题的最佳方法是使用弱表，这是一种通过弱引用实现的数据结构。弱表由弱对（weak pair）组成，其中第一个元素（键）由弱引用维护，第二个元素（值）由普通引用维护。这样，向对象添加property不会阻止其被收集。

然而，弱表中的循环问题仍然存在于大多数编程语言中：键和值之间存在循环引用，即使客户端程序没有对它们的其他引用，也会阻止收集循环中的元素。这些循环的常见情况是值引用它自己的键。例如，property表（使用弱表实现）可以将函数与其各自的模块相关联，以便它可以说明给定函数属于哪个模块。由于每个模块都会引用其所有函数，此property表中的任何键或值永远不会被收集。这最终会造成大量的内存浪费，并给使用弱表带来困难。在Java¹⁰和Lua¹¹等编程语言中可以发现此问题。通过Lua的讨论列表，我们可以看到与此问题相关的频繁抱怨。

这个问题的解决方案可以在Hayes¹²提出的一种称为ephemerons的机制中找到。Jones¹³独立为Haskell¹⁴编程语言开发了一种类似的解决方案，其核心思想与ephemerons机制相同。

基于Haskell的成功，我们为Lua设计并实现了该机制的改编版。作为起点，我们仔细研究了Hayes的著作[^Hayes 1997]中描述的算法。在研究该机制时，我们很好奇为什么大多数编程语言都没有实现该机制，以及实现它的影响是什么。之后，我们开发了LuaGC的改编版，以衡量这种影响。我们的目标是表明使用ephemerons可以轻松解决Lua弱表中的循环问题。通过这样做，我们能够改进弱引用机制。

2 Weak Tables

弱表是由弱对组成的数据结构。在弱对中，第一个元素（键）由弱引用保存，而第二个元素（值）由普通引用保存。在Java中，弱表由WeakHashMap类使用弱引用实现。在Lua中，弱表是一种原始机制（可用于在需要时实现常规弱引用）。然而，在Lua中，我们不仅可以构建包含弱对的弱表，还可以构建具有强键和弱值或弱键和弱值的弱表。

在Lua中，每个表都有一个控制其行为的元表。元表中的每个字段控制表的一个特定方面。字段__mode是一个控制表的weakness的字符串。如果此字符串包含字符"k"，则键为弱；如果它包含字符"v"，则值为弱；如果该字符串同时包含"k"和"v"，则键和值都为弱。Code 1展示了如何在Lua中创建由弱对组成的弱表。

-- Code 1 Creating a weak table in Lua.
 a = {}  -- a regular table
 b = {}  -- its metatable
 setmetatable(a, b)
 b.__mode = "k"  -- makes 'a' weak

大多数弱引用的典型用途涉及弱表。在弱引用（和弱表）最相关的应用中，我们重点介绍以下内容：

• 循环数据结构的收集——纯引用计数（reference-counting）GC无法回收循环数据结构。根据Brownbridge¹⁵的说法，这一缺陷是开发弱引用的最初动机。只需用弱引用替换普通引用，使每个循环至少有一个弱引用，即可轻松克服这一缺陷。随着tracing GC的出现，这种用法已变得过时。

• 缓存——频繁使用大型数据结构的应用程序可以通过将这些结构驻留在内存中来显著提高其性能。但是，这可能会导致内存快速耗尽。弱表提供了一种简单的解决方案来实现自动管理的缓存，只要内存不紧缺，它就会保留数据。

  根据文献¹⁶¹⁷所说，缓存的常见用途是记忆函数。通过保存其结果，可以显著减少处理复杂函数所需的计算工作量。当使用相同参数重新调用该函数时，它只会返回保存的值。在长期运行的应用程序中，记忆函数使用的存储空间可能会增长到令人望而却步的水平。在这种情况下，使用弱表可以透明地保存最近（可能也是最频繁）访问的值，而不会影响内存可用性。

• 弱集——弱集可以理解为一组对象，这些对象与该集合的相关性不会产生对该对象的引用。当对象必须作为一个组进行处理，但又不干扰其生命周期时，可以使用弱集作为一种实现解决方案。一个常见的例子是观察者设计模式，它定义了对象之间的一对多依赖关系，这样当一个对象改变状态时，它的所有依赖者都会收到通知并自动更新¹⁸。此通知由需要了解其观察者的被观察对象完成。在松散耦合的应用程序中，这些引用不应该妨碍观察者的收集。使用弱表来保存观察者集并不会妨碍它们被收集。

• Finalization——弱引用通过通知机制进行扩展，可以用于通知客户端程序已收集对象，最终执行与此类事件相关的例程（routine）。这称为基于容器的finalization，与实现面向对象finalization的class instance finalizer形成对比¹⁹²⁰。

• Property表——弱表可用于向对象添加任意property，即，它们可以表示property表。使用弱表表示property表的好处在于，在大多数情况下，向对象添加property不会改变其收集时间。例如，考虑图1中的表。在此表中，每个键都有一个对对象的弱引用，每个相应的值都有对此对象额外属性的普通引用。如果从键到对象的引用是普通的，那么在表中插入新的键/值对这一简单事实就会阻止收集由该键引用的对象。当从键到对象的引用是弱的，只要客户端程序不再使用对象，就可以收集它们。

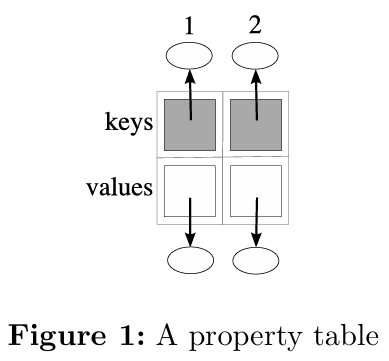
理想情况下，弱表中的键/值对只需在可以从表外部的某个位置直接或间接访问其键时才需要保留。（如果某个键由某个外部对象引用，则该键是直接可访问的。如果某个键由某个（键可直接或间接访问的）值引用，则该键是间接可访问的。）但是，大多数编程语言的实现并不表现这种行为。当某个entry的值部分直接或间接引用某个键时，就会出现问题，从而在其表内形成循环或在不同弱表的元素之间形成循环。图2中所示的表显示了这个问题。由于元素1的自引用（值指向其键）以及元素2和3创建的循环，这些元素引用的对象永远不会被收集。即使没有循环，对象的收集也可能需要比预期更多的时间。考虑元素4和5，其中元素4的值引用元素5的键。通常，GC只能在元素4被移除的周期之后的周期中移除元素5。具有n个元素链的弱表将需要至少n个循环才能完全收集。有人可能会认为将值从强更改为弱会有所帮助，但这是不正确的。考虑一个property表和一个仅作为此表中的值存在的对象。如果值对对象的引用为弱，则表示可以收集该对象。但是，相应的键可能处于活动状态，并且仍然可以使用该键搜索值（对象）。

当将弱表用作处理记忆函数的缓存时，也会出现循环。假设我们要创建常量函数：给定一个值，创建一个始终返回该值的函数。在Lua中，此函数的实现可以是：

function K(x)
    return function () return x end
end

如果我们想要记忆这个函数（这样就不需要为已经处理过的值重新创建这个函数），我们需要一个表映射x（键）到K(x)（值）。请注意，值是一个包含对x的引用的函数。这样，键和值都永远不会被收集。

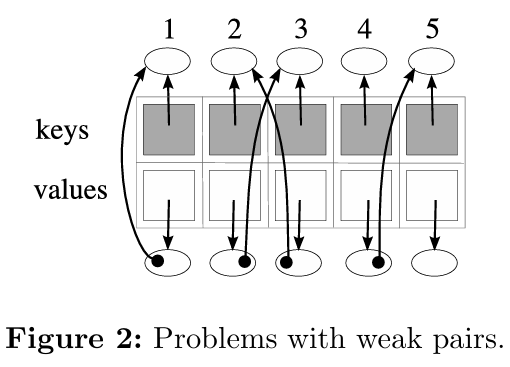
Java和Lua等编程语言都面临弱表循环的问题。Java的WeakHashMap API中有一条实现说明，指出“应注意确保值对象不会直接或间接强引用其自己的键，因为这将阻止键被丢弃”²¹。

3 Ephemerons

Hayes²²首次提出了一种解决弱表中循环问题的有趣方法，即使用ephemeron代替弱对。ephemeron是弱对的改进，其中的键和值都不能归类为弱或强。键的连通性（connectivity）决定了值的连通性，但值的连通性不会影响键的连通性。根据Hayes的说法，当GC为ephemeron提供支持时，它会分为三个阶段而不是两个（标记和清除）。接下来我们考虑第一和第二阶段，因为它们与我们的工作最相关。第三阶段的详细信息可以在Hayes²³的著作中找到。

在第一阶段，跟踪对象图，跟踪它们之间的引用。每当发现一个ephemeron时，收集器不会跟踪ephemeron的字段，而是将该 ephemeron插入队列中以供稍后处理。此队列中的ephemeron可能包含或不包含可访问的entry。

在第二阶段，收集器扫描ephemeron队列。当ephemeron的键已被到达时，将跟踪相应的值——如果键是可到达的，则程序的某些部分可能会请求该值。任何键尚未到达的ephemeron可能包含或不包含可到达的值；这些ephemeron将保留在队列中以供将来检查。现在我们有两组ephemeron，一组具有可到达的键，一组没有。第一组是按照与非ephemeron对象组相同的方式追踪。因为键已经到达并被跟踪，只需要跟踪值。但是，值可以包含对一些仍在队列的ephemeron的键的引用，将使这些键可访问。当发生这种情况时，需要重新检查队列。除此之外，可以找到额外的ephemeron。在这种情况下，它们被插入到队列中。

这个过程一直持续到队列中只有没有可到达的键的ephemeron。当队列收敛到这样的集合时，收集器可以回收这些ephemeron占用的内存。第二阶段的算法的伪代码如Code 2所示。

Hayes²⁴中提到，在第三阶段，收集器从仍在队列中的ephemeron开始追踪剩下的对象。这一阶段遇到的任何ephemeron被当作普通对象处理，并且所有字段都被追踪。

-- Code 2 Second phase of the ephemeron’s collection algorithm
while TRUE do
	for all e ∈ ephemeron-queue do
		if key(e) is marked then
			put(reachable-value, e)
		else
			put(unreachable-value, e)
		end if
	end for
	ephemeron-queue ⟸ unreachable-value
	if reachable-value is not empty then
        for all e ∈ reachable-value do
            trace(value(e))
		end for
		make-empty(reachable-value)
	else
		return
	end if
end while

Haskell编程语言定义了弱引用的语义，基于类似ephemeron的键/值对。我们的工作表明，通过修改GC算法，可以轻松地将ephemeron纳入目前的Lua的实现中。下一节将介绍我们如何实现ephemeron机制并测量了其效率和有效性。

4 Eliminating Cycles

正如我们在第2节中看到的，大多数弱引用的使用都涉及弱表。然而，循环问题给弱表的使用带来了障碍，因为它可能导致内存丢失或内存回收延迟。虽然在编程语言社区中并不为人所知，但ephemeron机制是解决此问题的一种非常合 理的方法。因此，我们决定调整Lua的GC算法以支持此机制，并衡量这样做的影响。

基本上，ephemeron由一个键/值对组成；这些键/值对不一定存储在表中。但是，由于我们在弱表中遇到循环时需要使用ephemeron，考虑ephemeron而不是单个键/值对是合理的。ephemerons表是在Lua中实现ephemeron的好方法，因为表是Lua的主要数据结构，并且Lua通过弱表提供对弱引用的支持。在我们的方法中，具有弱键和强值的弱表是ephemerons表。我们没有包含新类型的表，而是简单更改了垃圾收集算法。这样，在新的实现中，要创建ephemerons表，你只需以通常的方式创建一个具有弱键和强值的弱表。本节展示了这种弱表的旧实现与新实现（ephemerons表）之间的效率测量。

现在让我们看看它是如何工作的。Code 3展示了在表et（一个ephemerons表）中创建的简单循环。在这个循环中，第一个entry的值引用了第二个entry的键。如果使用具有弱键的弱表，则此循环永远不会被收集。创建循环后，显示调用GC。因为我们使用的是ephemerons表，所以循环将被收集，并且在执行结束时，变量count的值将为零。

4.1 Implementation

在讨论实现之前，我们将花一些时间来描述Lua GC。

Lua垃圾收集器实现了三色标记增量算法²⁵。此算法将跟踪阶段（检测到（非）垃圾时）与程序执行【脚注1】交错进行。在三色标记算法中，收集器可以描述为跟踪对象并为它们分配颜色的过程。一开始，所有对象都涂成白色。当收集器跟踪引用图时，它会为每个跟踪的对象分配黑色。

脚注1：有关GC算法和技术的更多信息，请参阅Wilson²⁶的著作。

-- Code 3 Example of how an ephemerons table works.
et = {}
mt = {}
setmetatable(et, mt) 
-- sets the table to be an ephemerons table,
-- in the new implementation.
mt.__mode = "k"

a = {}
b = {}
et[a] = b
et[b] = a
a = nil
b = nil
collectgarbage()
count = 0
for k,v in pairs(et) do
	count = count + 1
end
print(count) -- 0

到收集结束时，程序可访问的对象必须被涂成黑色，所有白色对象都将被删除。但是，由于程序和GC的执行是交错的，我们还需要考虑中间阶段。此外，程序不能以【收集器无法找到所有可访问对象】的方式更改引用图。为了防止这种情况，三色标记算法使用第三种颜色灰色来表示可能尚未跟踪其后代的已访问对象。这样，在跟踪过程中，只要发现一个对象，它就会被染成灰色。当跟踪到所有后代时，该对象就会被染成黑色。直观地看，跟踪在灰色对象的wavefront中进行，灰色对象将白色（未到达）对象与黑色对象分开，并且有一个不变量，即黑色对象永远不会引用白色对象。但是，程序仍然可以需要创建一个从黑色指向白色对象的指针，这违反了不变量。为了防止这种情况，收集器使用write barrier：每当程序尝试将对白色对象的引用写入黑色对象时，要么原点变为（从黑色）灰色，要么目标变为（从白色）灰色。

Lua垃圾收集分为四个阶段。在第一阶段，收集器跟踪引用图并给对象着色。此阶段与程序的执行交错进行。第二阶段称为原子阶段，当多个操作在一个步骤中执行时——一些垃圾收集器的操作不能与程序的执行交错（例如，清除弱表）。第三阶段，也是增量阶段，收集器释放白色对象占用的内存。最后，在第四阶段，finalizer被与程序的执行交错调用。为了简化对GC行为的理解，我们将在讨论中考虑两个阶段：原子阶段，由前面提到的第二阶段组成；以及非原子阶段，由第一、第三和第四阶段组成。

在ephemeron的收集算法中，垃圾收集器首先跟踪对象图。当它找到一个ephemeron时，垃圾收集器不会立即跟踪ephemeron的字段，而是将此ephemeron插入队列中以便稍后处理，然后继续跟踪阶段。在我们的例子中，我们需要一个数据结构来表示ephemerons表的队列。Lua GC的原始实现有一个单独的数据结构来存储所有三种弱表，即弱列表。在我们的GC实现中，此列表被分成三个单独的列表，每种弱表一个。仅存储弱键的弱表的列表称为ephemeron列表，因为所有这种类型的表都表示一个ephemerons表。在跟踪阶段，每当垃圾收集器找到一个ephemerons表时，它都会将此表插入到ephemeron列表中。

为了实现ephemeron机制，我们在GC的阶段添加了新操作。首先，如前所述，只要找到ephemerons表，它就会被列入ephemeron列表中。ephemerons表中的entry不会被跟踪，无论是键还是值。（请记住，在原始机制中，每个键/值对代表一个ephemeron。）这就是第一阶段添加的全部内容。

随后，收集器进入原子阶段，此时多个操作在一个步骤中执行。我们为该阶段实现了两个新函数：traverseephemeron，用于跟踪ephemeron列表；convergeephemerons，用于调用第一个函数来收敛ephemeron列表。这些函数的伪代码可在Code 4中找到。函数traverseephemeron跟踪ephemerons表中的所有entry。如果某个entry的键被标记，即已到达该键，则标记相应的值。函数traverseephemeron返回一个布尔值，由Code 4中的变量b定义。如果来自ephemerons表的任何值已被标记，则此布尔值为真，否则为假。

convergeephemerons函数调用traverseephemeron。如果此函数返回true，即如果某个值已被标记，则前者调用收集器原始实现中的函数propagateall。此函数未经修改。其职责是跟踪程序的引用图，并根据三色标记算法扩展灰色对象的屏障。请注意，在之前执行traverseephemeron时，标记了ephemerons表的值。因此propagateall将标记被这些值直接或间接引用的对象。由于这些新标记的对象可能引用ephemerons表中的键，函数convergeephemerons再次调用traverseephemeron。当没有标记任何值时，traverseephemeron返回false。如果在跟踪所有ephemerons表后没有标记任何值，则convergeephemerons终止执行。函数convergeephemerons和traverseephemeron将原始ephemeron机制的第二阶段适配到Lua GC。

-- Code 4 Pseudo-code for convergeephemerons and traversephemeron
 function convergeephemerons(ephemeron)
 while TRUE do
 	changed ⟸ FALSE
 	for all e ∈ ephemeron do
 		if traverseephemeron(e) then
 			changed ∈ TRUE
 			propagateall(...)
 		end if
 	end for
 	if not changed then
 		break
 	end if
end while
            
 function traverseephemeron(e)
 b ⟸ FALSE
 for all pair ∈ hash(e) do
 	if key(pair) is marked then
 		mark the value
 		b ⟸ TRUE
	end if
end for
return b

在执行convergeephemerons之后，并且仍然处于原子阶段时，收集器调用cleartable函数作为propagateall，这个函数也属于收集器的原始实现。函数cleartable从弱表（包括具有弱键和强值的ephemerons表）中删除无法访问的entry。最终，收集器继续到最后阶段，释放内存并执行finalizer。此阶段未修改。

5 Efficiency Analysis

在本节中，我们分析了ephemerons表的收集和仅具有弱键的弱表的收集（在原始GC中实现）。

考虑一个创建\(K_e\)个ephemerons表的程序A和一个创建\(K_f\)个弱表的程序B。程序A使用经过调整的GC，其中具有弱键和强值的弱表表示ephemerons表，而程序B使用原始GC。假设A中的每个ephemerons表在其哈希部分中有\(e_h\)个条目，在其数组部分【脚注2】中有\(e_a\)个条目。还假设B中的每个弱表在其哈希部分中有\(f_h\)个条目，在其数组部分中有\(f_a\)个条目。并考虑\(e_n=e_a+e_b\)和\(f_n=f_a+f_b\)。

脚注2：Lua中的每个表都有两部分：由自然数索引的数组部分和由其他对象索引的哈希部分。

在处理ephemerons表或弱表时，一些GC函数对于收集性能至关重要。在经过调整的GC中，这些函数是：

• traversetable：跟踪一个表以标记其键和值；

• traverseephemeron：追踪一个ephemerons表以标记相关相应键已到达的值；

• cleartable：删除在跟踪阶段未到达的ephemerons表和弱表的entry。

从这些函数中，只有traversetable是在非原子阶段执行的。该函数为每个普通的、只有弱值的弱表或 ephemerons表执行一次。当表是ephemerons表时，traversetable将控制权传递给traverseephemeron。最后一个函数有两个循环，一个用于迭代数组部分，另一个用于迭代表的哈希部分。由于所有数值键都是强的，数组部分中的所有值都被标记。在哈希部分，每当标记一个键时，就会标记该值，但不跟踪该值。程序A的traversetable成本为\(O(e_n)\)。改造后的GC与原版GC的区别在于，后者没有traverseephemeron函数，traversetable函数跟踪所有表。这样，程序B的traversetable成本为\(O(f_n)\)。

在跟踪弱表和ephemerons表之后，新GC的原子阶段将执行convergeephemerons，它会不断调用traverseephemeron，直到没有值被标记。现在我们需要考虑convergeephemerons的最好以及最坏情况。在最好情况下，没有值直接或间接指向ephemerons表中的键。在这种情况下，最多对ephemeron列表进行两次迭代：第一次用于标记已达到其键的值，第二次用于在第一次迭代中标记某个值的情况下。在最好情况下（对于程序A），convergeephemerons的成本为\(O(K_e×e_n)\)。

最坏的情况发生在存在键值链时。图3描述了这种链的一个示例。假设客户端程序对第一个ephemerons表中的第一个值有强引用。请注意，每个ephemerons表中的值都指向下一个表的键，从而形成一个链。在这种情况下，convergeephemerons中的循环执行\(K_e+1\)次：每个值标记一次，最后一次不修改任何内容。在这个最坏情况下，convergeephemerons的成本为\(O(K_e^2+(K_e×e_n))\)。

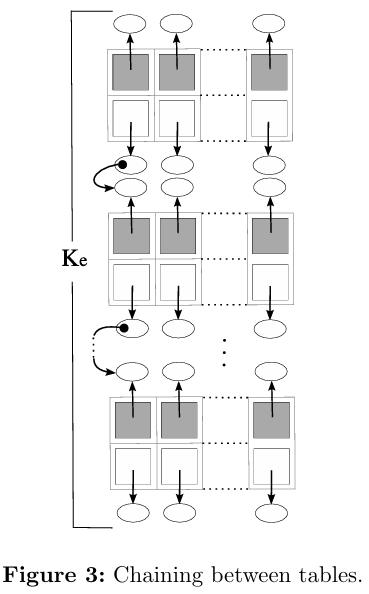
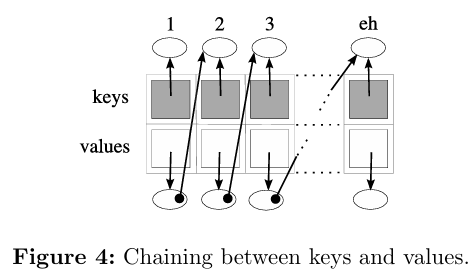
图4描述了另一个最坏情况的例子，其中来自同一张表的键和值是链在一起的。convergeephemerons中的循环将执行\((2×e_h)+1\)次：每个值标记一次，最后一次不修改任何内容。这样，convergeephemerons的成本为\(O(e_n^2+(K_e×e_n))\)。

函数cleartable在两种实现中具有相同的行为。对于程序A，此函数的成本为\(O(K_e×(e_n))\)；对于程序B，为\(O(K_f×(f_n))\)。结果是，程序A中ephemerons表的收集成本在最佳情况下为\(O(K_e×(e_n))\)，程序B中为\(O(K_f×(f_n))\)。考虑程序A和B相同，只是A使用改进的垃圾收集器。这种情况下，每个程序的收集成本是相同的。

然而，在两种最坏情况下，程序A的收集成本都是平方的。更准确地说，对于图3中的情况，成本为\(O(K_e×(e_n))\)，而对于图4中的情况，成本为\(O(e_h×(e_n))\)。表之间或键和值之间的链很少发生，但一旦发生就会严重影响效率。由于程序B使用原始垃圾收集器，它仍然是线性的。但是，请注意，程序B中不会收集弱表中的循环，这可能会导致内存丢失（这可能比效率损失更严重）。

5.1 Efficiency Measurements

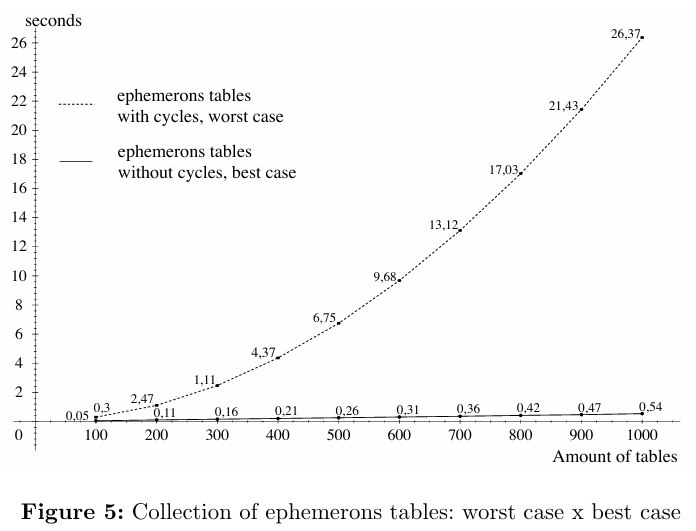
我们执行了两项测试，以测量扩展GC的效率。第一项测试比较了没有循环（或链）的ephemerons表的收集和有链的ephemerons表（如图3）的收集。我们从不同数量的无循环的ephemerons表开始，范围从100到1000个表。每个表有500个entry。在对无循环的ephemerons表执行测试后，我们创建了相同数量的具有链的ephemerons表并测试了它们的收集。因此，我们可以比较最好和最坏情况的执行时间。结果如图5所示。正如预期的那样，表示带有链的ephemerons表的曲线与二次函数的曲线相似。在最坏的情况下，GC的效率会受到很大影响。但是，由于我们使用的是ephemerons表而不是弱表，因此所有循环都会被收集。

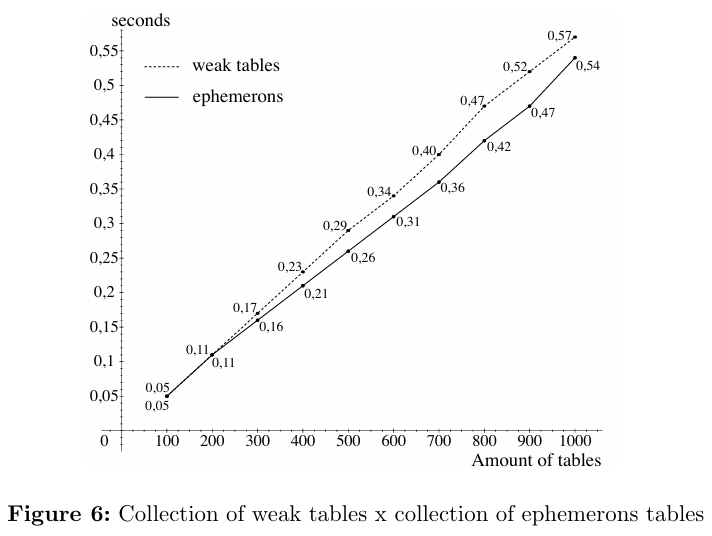
第二次测试的目的是比较改造后的GC的效率与原始GC的效率。这一次，只有弱键的弱表（在改造后的GC中被视为ephemerons表）没有循环。此测试与第一次测试使用相同数量的表执行，首先仅使用弱表（原始实现），然后仅使用ephemerons表（改造实现）。结果如图6所示。请注意，收集无循环的ephemerons表的时间和收集弱表的时间几乎没有差别。我们认为收集ephemerons表的结果更好是因为测试执行中的一些噪音，而不是ephemerons表的收集更加高效。我们可以得出这样的结论：在缺乏循环的情况下，我们对ephemerons机制的实现与弱表的实现效率相同。

6 Conclusion

弱表是实现弱引用的好方法。事实上，大多数弱引用的使用，如property表、弱集和缓存，都涉及弱表。然而，弱表中的循环问题仍然存在于大多数编程语言中。这可能会导致内存丢失或内存回收延迟。虽然在程序员中并不出名，但ephemerons机制对于这一问题是一个非常合理的解决方案。

因为只有在弱表的上下文中ephemerons才是必要的，所以我们认为考虑ephemerons表而不是独立的键/值对更为合理。我们可以在Lua GC中轻松地实现对原始ephemerons机制的改造。在没有循环的情况下，我们的实现与弱表的实现一样高效。当循环确实存在时，ephemerons表能够收集它们。综上所述，我们认为这一机制可以很容易地在任何编程语言实现，就像在Lua中一样。

7 Acknowledgments

我们衷心感谢审稿人的宝贵建议。

---

1. Atkins, M. C., Nackman, L. R.: “The Active Deallocation of Objects in Object-Oriented System”; Software: Practice and Experience, 18, 11 (1988), 1073-1089.↩︎

2. Boehm, H.: “Destructors, Finalizers, and Synchronization”; Proc. of the 30th ACM SIGPLAN-SIGACT symposium on Principles of Programming Languages (2003), 262-272.↩︎

3. Dybvig, R. K., Bruggeman, C., Eby, D.: “Guardians in a Generation-based Garbage Collector”; Proc. of the ACM SIGPLAN ’93 Conference on Programming Language Design and Implementation (1994), 207–216.↩︎

4. Hayes, B.: “Finalization in the Collector Interface”; Proc. of the ’92 In ternational Workshop on Memory Management, London (1992), 277–298.↩︎

5. Legal, M. A.: “Finalizadores e Referˆencias Fracas: Interagindo com o Coletor de Lixo”; PhD thesis, Informatics Department, Pontifical Catholic University of Rio de Janeiro (2005).↩︎

6. Bloch, J.: “Effective Java Programming Language Guide”; Prentice Hall, f irst edition (June 2001).↩︎

7. Boehm, H.: “Destructors, Finalizers, and Synchronization”; Proc. of the 30th ACM SIGPLAN-SIGACT symposium on Principles of Programming Languages (2003), 262-272.↩︎

8. Xerox Palo Alto Research Center (PARC): “InterLISP Reference Manual”; Palo Alto, CA (October 1985).↩︎

9. Rees, J. A., Adms, N. I., Meehan, J. R.: “The T Manual”; Yale University, Computer Science Department, fourth edition (January 1984).↩︎

10. Sun Microsystems: “JavaTM Platform Standard Edition 6.0: API Specification”; (2006).↩︎

11. Ierusalimschy, R.: “Programming in Lua”; Lua.org, second edition (2006).↩︎

12. Hayes, B.: “Ephemerons: a New Finalization Mechanism”; In Proc. of the 12th ACM SIGPLAN Conference on Object-Oriented Programming, Systems, Languages, and Applications, New York, NY (1997), 176–183.↩︎

13. Jones, S. P., Marlow, S., Elliott, C.: “Stretching the Storage Manager: Weak Pointers and Stable Names in haskell”; Lect. Notes Comp. Sci. 1868, Springer (1999), 37-58.↩︎

14. The Glasgow Haskell Compiler user’s guide, version 6.2; http://www.haskell.org/ghc, last viewed in April 2nd, 2007.↩︎

15. Brownbridge, D. R.: “Cyclic Reference Counting for Combinator Machines”; Proc. of the ACM Conference on Functional Programming Languages and Computer Architecture, New York, NY (1985), 273–288.↩︎

16. Ierusalimschy, R.: “Programming in Lua”; Lua.org, second edition (2006).↩︎

17. Jones, S. P., Marlow, S., Elliott, C.: “Stretching the Storage Manager: Weak Pointers and Stable Names in haskell”; Lect. Notes Comp. Sci. 1868, Springer (1999), 37-58.↩︎

18. Gamma, E., Helm, R., Johnson, R., Vlissides, J.:“Design Patterns: Elements of Reusable Objetct-Oriented Software”; Addison Wesley (1995).↩︎

19. Hayes, B.: “Ephemerons: a New Finalization Mechanism”; In Proc. of the 12th ACM SIGPLAN Conference on Object-Oriented Programming, Systems, Languages, and Applications, New York, NY (1997), 176–183.↩︎

20. Jones, S. P., Marlow, S., Elliott, C.: “Stretching the Storage Manager: Weak Pointers and Stable Names in haskell”; Lect. Notes Comp. Sci. 1868, Springer (1999), 37-58.↩︎

21. Sun Microsystems: “JavaTM Platform Standard Edition 6.0: API Specification”; (2006).↩︎

22. Hayes, B.: “Ephemerons: a New Finalization Mechanism”; In Proc. of the 12th ACM SIGPLAN Conference on Object-Oriented Programming, Systems, Languages, and Applications, New York, NY (1997), 176–183.↩︎

23. Hayes, B.: “Ephemerons: a New Finalization Mechanism”; In Proc. of the 12th ACM SIGPLAN Conference on Object-Oriented Programming, Systems, Languages, and Applications, New York, NY (1997), 176–183.↩︎

24. Hayes, B.: “Ephemerons: a New Finalization Mechanism”; In Proc. of the 12th ACM SIGPLAN Conference on Object-Oriented Programming, Systems, Languages, and Applications, New York, NY (1997), 176–183.↩︎

25. Dijkstra, E. W., Lamport, L., Martin, A. J., Scholten, C. S., Ste ens, E. F. M.: “On-the-fly Garbage Collection: An Exercise in Cooperation”; Communications of the ACM, 21, 11 (November 1978, 966-975.↩︎

26. Wilson, P. R.: “Uniprocessor Garbage Collection Techniques”; Proc. of the 1992 International Workshop on Memory Management, Saint-Malo, France (1992), 1-42↩︎